Model concept, solver and details - IMACLIM
| Corresponding documentation | |
|---|---|
| Previous versions | |
| Model information | |
| Model link | |
| Institution | Centre international de recherche sur l'environnement et le développement (CIRED), France, http://www.centre-cired.fr., Societe de Mathematiques Appliquees et de Sciences Humaines (SMASH), France, http://www.smash.fr. |
| Solution concept | General equilibrium (closed economy) |
| Solution method | SimulationImaclim-R is implemented in Scilab, and uses the fonction fsolve from a shared C++ library to solve the static equilibrium system of non-linear equations. |
| Anticipation | Recursive dynamics: each year the equilibrium is solved (system of non-linear equations), in between two years parameters to the equilibrium evolve according to specified functions. |
The Imaclim-R model (Sassi et al., 2010 sassi2010im; Waisman et al., 2012[[CiteRef::waisman2012th]), is a multi-region and multi-sector model of the world economy. It combines a Computable General Equilibrium (CGE) framework with bottom-up sectoral modules in a hybrid and recursive dynamic architecture. Furthermore, it describes growth patterns in second best worlds with market imperfections, partial uses of production factors and imperfect expectations.
A hybrid modelling structure to study the interactions between the evolutions of energy systems and economic growth
Assessing the intertwined evolution of technical systems, energy demand behaviors and economic growth, as well as the costs and benefits of transitions to low carbon economies is a major challenge for economic modeling. Ideally, models should (i) be framed in a consistent macroeconomic framework, (ii) include the relevant technical constraints in each sector, such as views about the direction of technical change, (iii) capture the key relationships between economic activity and the environment, e.g., energy and natural resources consumption or greenhouse gases emissions, (iv) have a horizon long enough to assess ?sustainability?- a long-term horizon which also implies, incidentally, that the model must be able to represent structural and technical change, yet (v) recognize short-term economic processes critical for assessing transition pathways, such as market imbalance and rigidities.
No model in existence today meets all of these specifications. In fact, current models can be classified along two major fault lines: bottom-up vs. top-down, and long-term vs. short-term.
By design, computable general equilibrium (CGE) models which are classed as top-down, provide a comprehensive macroeconomic framework (i); but they typically adopt oversimplified representations of technical constraints and then fail to explicitly include their interactions with growth trajectories. Conversely, bottom-up engineering models provide a detailed account of technical potentials and limitations (ii), but their macro-engine, if existing at all, is most often rudimentary. Emerging ?hybrid? models developed in the context of climate policy assessment are steps towards addressing these drawbacks. A similar dichotomy occurs with regard to the time horizon. Growth models in the Solow tradition are designed to capture key features of long-term development paths (iv), but they do not include short- or medium-term economic processes such as market rigidities. On the other hand, short-term models (econometric or structural) will meet requirement (v) but are not designed to project far into the future. Emerging models thus include short/medium-term processes into their analysis of growth in the long-run, although this remains an open research field.
The IMACLIM modelling platform, developed at CIRED, is a step towards the five-point specification outlined above. It comprises a hybrid structure that combines a multi-sectorial top-down macroeconomic framework with a bottom-up modules for each sector. A key feature of IMACLIM is its dual representation of economic flows in monetary flows (e.g., euros or dollars) and in physical quantities (e.g., MToe for energy, passenger.km for mobility). This dual representation allows for explicit representation of the material and technological content of economic activity and endogenization of the interactions between these technical dimensions and growth trajectories: the projected economy is supported by a realistic technical background (in the engineering sense) and, conversely, that projected technical systems are bounded by realistic economic flows and consistent sets of prices. This modeling principle facilitates interaction between technical and economic considerations and allows in particular a detailed representation of sectorial characteristics.
A recursive and modular simulation architecture capturing inertias and imperfect foresight
IMACLIM-R models the evolution of the economy over the period 2001-2100, in one year time steps.
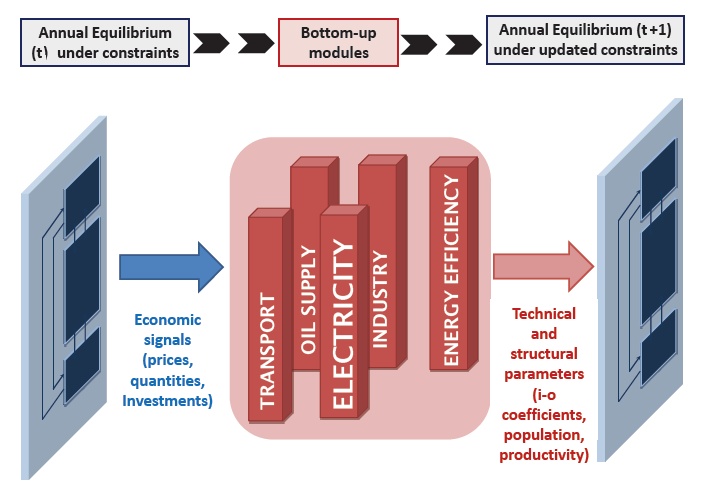
Technically, the model can be labelled as a recursive dynamic simulation framework, since it generates an energy-economy trajectory by solving a sequence of yearly static equilibria of the economy, interlinked by dynamic modules. The recursive structure organizes a systematic exchange of information between a top-down annual static equilibrium providing a snapshot of the economy, and bottom-up dynamic modules providing information on the evolution of technical parameters between each annual equilibria (Figure 1.1.1).
Figure 1.1.1 The recursive and modular architecture of the Imaclim-R hybrid model.
For each annual static equilibrium, domestic and international markets ? besides markets for factors such as capital and labour ? are fully cleared by a unique set of relative prices that depend on the behaviours of representative agents (producers, households, states) on the demand and supply sides. The calculation of this annual equilibrium determines the following variables: relative prices, wages, labour, quantities of goods and services including energy, value flows, physical flows and capacity utilization.
Households choose their consumption of goods and services to maximize their current utility under both income and time constraints; the former is the sum of wages, capital returns and transfers whereas the latter controls the total time spent in transportation.
The behaviour of producers is not represented by a flexible production function allowing for substitution between factors, as it is in common practice. Instead, these substitutions occur between two equilibria in sector-specific dynamic modules. Producers are therefore assumed to operate under short-run constraints of (i) a fixed maximal production capacity Cap'k,i, defined as the maximum level of physical output achievable with the equipment installed, and (ii) fixed input-output coefficients representing that with the current set of installed technologies, producing one unit of a good i in region k requires fixed physical amounts IC'j,i,k of intermediate goods j and of labour l'k,i. In this context, the only room for manouvre producers have is to adjust the utilisation rate Q'k,i'/Cap'k,i according to the relative market prices of inputs and output, taking into account decreasing static returns when capacity utilization approaches saturation [1]. Producers determine their prices using a marginal rate over and above production costs (mark-up) to capture the effect of imperfect competition [2]. This represents a different paradigm from usual production specifications e,g, with constant elasticity of substitution KLEM production functions, since the ?capital? factor is not always fully utilized.
Total demand for each good (the sum of households? consumption, public and private investments and intermediate uses) is satisfied by a mix of domestic production and imports [3]. All intermediate and final goods are internationally tradable. Domestic as well as international markets for all goods are cleared (i.e. no stock is allowed) by a unique set of relative prices and this determines the utilization rate of production capacities [4].
Between annual equilibria, dedicated modules describe the investments choices and the evolution of preferences, techniques and land uses; thereby updating the next equilibrium parameters at t+1 (installed production capacities, households equipment, the installed technologies represented by the input-output coefficients?).
The equilibrium values of all variables from previous equilibria serve as signals for agents? decisions represented in the dynamic modules. Therefore decisions are taken with no perfect foresight of future values.
Within the dynamic modules, technical choices are available, however only marginal changes in the input-output coefficients embodied in existing equipment vintages (arising from past technical choices) are possible/allowed.
The dynamic modules represent the evolution of technical coefficients resulting from agents? microeconomic decisions on technological choices, under the limits imposed by the innovation possibility frontier, IPF, (Ahmad, 1966). They embed a) sectoral level information on economies of scale, learning-by-doing mechanisms and saturation in efficiency progress, and b) expert views about the asymptotes of ultimate technical potentials, the impact of incentive systems, and the role of market or institutional imperfections. The new investment choices and technical coefficients are then sent back to the static module in the form of updated production capacities and input-output coefficients to calculate the t+1 equilibrium.
This general putty-clay representation with fixed technical content of installed capital, is critical to the representation of inertia in technical systems. It allows for distinction between short-term rigidities and long-term flexibilities (Johansen, 1959).
Summary
The IMACLIM-R model endogenizes the rate and direction of technical change by representing the bottom-up impact of investment decisions on the deployment of technical systems. The consistency of the top-down/bottom-up communication is guaranteed by a hybrid structure representing the economy in money values and physical quantities (Hourcade et al, 2006). This dual accounting, following the Arrow-Debreu framework (Arrow and Debreu, 1954), ensures that the projected economy is supported by a realistic technical background and, conversely, that projected technical systems correspond to realistic economic flows and consistent sets of relative prices.
Practical implementation
Imaclim-R is implemented in Scilab, and uses a C solver to solve the static equilibrium system of non-linear equations.
[1] Following (Corrado and Mattey, 1997), decreasing returns reflect the higher labor costs associated to overtime extra-hour, costly night work and increasing maintenance works when capacity utilization approaches saturation.
[2] The mark-ups are exogenous except in the energy sector where they are endogenous to reflect (a) the market power of fossil fuel producers, (b) specific pricing principles in the power sector (e.g., mean cost pricing), and (c) the different margins over the three inputs for liquid fuels production (oil, biomass, coal).
[3] For non-energy goods, we adopt Armington specifications (Armington, 1969) to capture the partial substitutability between domestic and foreign goods, while for energy goods (in MToe) physical accounting makes them fully substitutable.
[4] The partial utilization rate of production capacities allows the represention of operational flexibility through early retirement of those capacities which, although installed, are not used for actual production because they are not competitive in current economic conditions.