Electricity - DNE21+: Difference between revisions
No edit summary |
No edit summary |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{ModelDocumentationTemplate | {{ModelDocumentationTemplate | ||
|IsEmpty=No | |IsEmpty=No | ||
|IsDocumentationOf=DNE21 | |IsDocumentationOf=DNE21+ | ||
|DocumentationCategory=Electricity | |DocumentationCategory=Electricity | ||
}} | }} | ||
| Line 17: | Line 17: | ||
Electricity demand is modeled in a way that demand-supply is balanced. The demand is expressed by the load duration curves, representing four time periods, instantaneous peak, peak, intermediate, and off peak time periods, in accordance with the level of electricity demand. This enables appropriate evaluation of electricity system corresponding to the characteristics of individual power generation technologies such as the base power load power plants and the peak load power plants. | Electricity demand is modeled in a way that demand-supply is balanced. The demand is expressed by the load duration curves, representing four time periods, instantaneous peak, peak, intermediate, and off peak time periods, in accordance with the level of electricity demand. This enables appropriate evaluation of electricity system corresponding to the characteristics of individual power generation technologies such as the base power load power plants and the peak load power plants. | ||
For nuclear power generation, exogenous scenarios are assumed for nuclear power generation up to 2030. Some constraints are assumed that the power generation of nuclear would be capped at 50% of the total power generation amount and that an annual expansion of conventional nuclear power generation would be 0.33%, and the expansion rate of advanced | For nuclear power generation, exogenous scenarios are assumed for nuclear power generation up to 2030. Some constraints are assumed that the power generation of nuclear would be capped at 50% of the total power generation amount and that an annual expansion of conventional nuclear power generation would be 0.33%, and the expansion rate of advanced nuclear power generation would be 1%. As long as the constraints are obeyed, costs-efficient options are selected by the model. | ||
Latest revision as of 11:29, 30 August 2016
| Corresponding documentation | |
|---|---|
| Previous versions | |
| Model information | |
| Model link | |
| Institution | Research Institute of Innovative Technology for the Earth (RITE), Japan, http://www.rite.or.jp/en/. |
| Solution concept | |
| Solution method | |
| Anticipation | |
The modeled electricity generation options include: Coal power {low efficiency (subcriticality), mid-efficiency (supercriticality), high efficiency (extra supercriticality?IGCC/IGFC), and IGCC with pre-combustion CO2 capture}, Oil power {low efficiency (diesel generator, etc.), mid-efficiency (subcriticality), high efficiency (supercriticality), and CHP}, Synthetic oil power {mid efficiency, and high efficiency}, Natural gas power {low efficiency (steam turbine), mid-efficiency (conventional NGCC), high efficiency (high temperature NGCC), CHP, and oxy-fuel combustion}, Biomass power {low efficiency, and high efficiency}, Nuclear power {conventional, and next-generation (Generation IV, etc.)}, Hydro/geothermal power, Wind power, and Photovoltaics. In association with generation technologies, Power storage system for wind/PV, Hydrogen power, Electrical cable {conventional, superconducting high efficiency}, and CCS {post-combustion capture; applicable for coal, oil, synthetic oil, natural gas, biomass power} are also represented in DNE21+.
As shown above, each type of power generation technology has is classified according to level of energy efficiencies and facilities costs are differentiated corresponding to the level of efficiency. The different levels of generation efficiencies are assumed in order to represent the broader ranges in current generation efficiency levels in different countries (see Oda et al. 2012). Their technological progresses are assumed exogenously. Table 3 shows the assumptions on capital costs and the efficiency of electricity generation. Fossil fuel prices are endogenously determined within the model by using the relationship between the cumulative production of fossil fuels and production costs. However, the fossil fuel prices will be dominated not only by production prices, but also by speculation, etc. Therefore, the baseline fossil fuel prices are calibrated to meet the prices of the reference scenarios of the IEA WEO 2010 (IEA 2010b) over the assessment time periods, while the prices in the mitigation scenarios are endogenously determined by the cumulative amounts of production induced by levels of emission reductions or the MAC. DNE21+ also tracks investments by vintage capital stock.
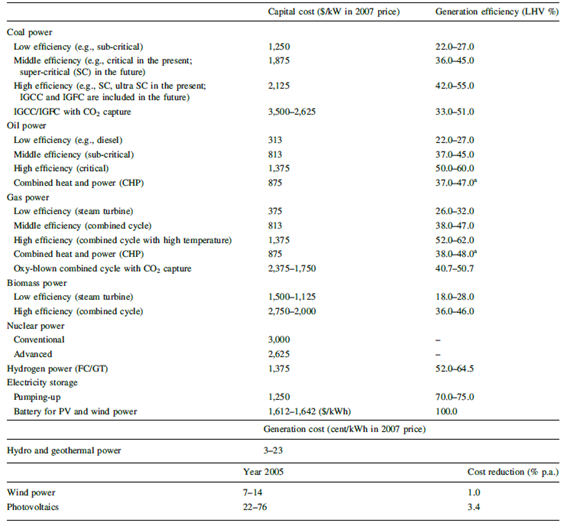Table 3 Capital costs and generation efficiency
- Some of capital costs and efficiency are shown in a range because they change over time.
Electricity demand is modeled in a way that demand-supply is balanced. The demand is expressed by the load duration curves, representing four time periods, instantaneous peak, peak, intermediate, and off peak time periods, in accordance with the level of electricity demand. This enables appropriate evaluation of electricity system corresponding to the characteristics of individual power generation technologies such as the base power load power plants and the peak load power plants.
For nuclear power generation, exogenous scenarios are assumed for nuclear power generation up to 2030. Some constraints are assumed that the power generation of nuclear would be capped at 50% of the total power generation amount and that an annual expansion of conventional nuclear power generation would be 0.33%, and the expansion rate of advanced nuclear power generation would be 1%. As long as the constraints are obeyed, costs-efficient options are selected by the model.