Transport - REMIND-MAgPIE
| Corresponding documentation | |
|---|---|
| Previous versions | |
| Model information | |
| Model link | |
| Institution | Potsdam Institut für Klimafolgenforschung (PIK), Germany, https://www.pik-potsdam.de. |
| Solution concept | General equilibrium (closed economy)MAgPIE: partial equilibrium model of the agricultural sector; |
| Solution method | OptimizationMAgPIE: cost minimization; |
| Anticipation | |
REMIND models the transport sector by using a hybrid approach combining top-down and bottom-up elements (see Figure 4<xr id="fig:REMIND_4"/>). Specifically, mobility demands for the 4 modeled transport sub-sectors (Passenger-light duty vehicles (LDV), Freight, Electric Rail, Passenger-Aviation and Buses) are derived in a top-down fashion, since they are input to a nested CES production function that ultimately produces GDP. For the LDV mode, three different technology options (internal combustion engine, battery electric vehicle, and fuel cell vehicle) compete against each other in a linear bottom-up technology model.
The transport sector requires input of final energy in different forms (liquids, electricity and hydrogen) and requires investments and operation and maintenance payments into the distribution infrastructure (infrastructure capacity grows linearly with distributed final energy) as well as into the vehicle stock. It generates emissions that go into the climate model and, depending on the scenario, can be taxed or limited by a budget. Furthermore, it is possible to consider taxes and subsidies on fuels. Material needs and embodied energy are not considered.
The main drivers/determinants of transport demand are GDP growth, the autonomous efficiency improvements (efficiency parameters of CES production function), and the elasticities of substitution between capital and energy and between stationary and transport energy forms. In more detail, mobility from the different modes comes as an input to a CES function, the output of which is combined with stationary energy to generate a generalized energy good, which is combined with labor and capital in the main production function for GDP. Finally, inside a model run, different final energy prices (due to climate policy, different resource assumptions, etc.) can lead to substitution of different transport modes inside the CES function, or a total reduction of travel demand (see Pietzcker et al. (2014a) for a comparison of the different contributions to transport mitigation). For passenger transport, we consider LDV (powered by liquids, electricity or hydrogen), Aviation and Bus (aggregated, only powered by liquids) and Electric Trains (only powered by electricity). For freight transport, there is only one generic mode based on liquid fuels. For the conversion technologies of primary energy sources into these secondary energy carriers, see Section Energy Conversion.
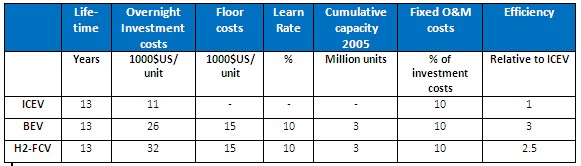
The distribution of vehicles inside the LDV mode follows cost optimization (perfect linear substitutability), although with different non-linear constraints (learning curve, upper limits of 70% on share of battery-electric vehicles and 90% on Fuel Cell vehicles) that in most realizations lead to a technology mix.
Efficiency, lifetime, investment costs, and fixed O&M costs parameters characterize all vehicle technologies. All these parameters, except investment costs for battery electric and fuel cell vehicles, are constant over time. Battery electric vehicles and fuel cell vehicles undergo learning-by-doing through a one-factor learning curve with floor costs that are asymptotically approached as cumulated capacity increases. Fuel prices are fully endogenous, as determined by the supply sector (intertemporal optimization with resource and capacity constraints as well as prices/constraints on emissions in policy scenarios).
Table 9. Overview of LDV technologies
<figure id="fig:REMINDtable_9">
 </figure>
</figure>