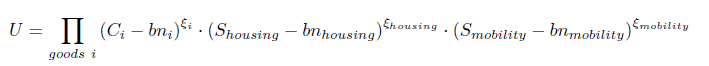Energy demand - IMACLIM
| Corresponding documentation | |
|---|---|
| Previous versions | |
| Model information | |
| Model link | |
| Institution | Centre international de recherche sur l'environnement et le développement (CIRED), France, http://www.centre-cired.fr., Societe de Mathematiques Appliquees et de Sciences Humaines (SMASH), France, http://www.smash.fr. |
| Solution concept | General equilibrium (closed economy) |
| Solution method | SimulationImaclim-R is implemented in Scilab, and uses the fonction fsolve from a shared C++ library to solve the static equilibrium system of non-linear equations. |
| Anticipation | Recursive dynamics: each year the equilibrium is solved (system of non-linear equations), in between two years parameters to the equilibrium evolve according to specified functions. |
Households final demand
Households' final demand for goods and services, including energy services, results from solving the current utility maximization program of a representative consumer for each region.
Income and savings
Household income in each region k is equal to the sum of (i) wages received from all sectors j of this region (we assume a non-mobile labor supply), (ii) dividends of the productive sectors that are equal to a fixed share of sectoral profits within each region (we don't take into account the holding of foreign capital and their returns), and (iii) public transfers.
Households' savings are a proportion of their income. Saving rates are taken as exogenous trends. By default, this trend is calibrated on results from the INGENUE model (Hairault and Kempf, 2002) that links savings behaviors to the dynamics of regional population pyramids.
Utility function
The arguments of the utility function U are the goods Ck,i produced by the agriculture, industry and services sectors, with basic needs bnk,i, and the services of mobility Sk,mobility (in passenger.kilometers) and housing Sk,housing (in square metres). Households thus make a trade-off between the consumption of different goods and services, including the purchase of new end-use equipment stocks.
Energy commodities are considered as production factors of mobility and housing services: they are not directly included in the utility function, but the associated energy burden weighs on the income constraint. Energy consumption for housing results from efficiency coefficients characterizing the existing stock of end-use equipment per square meter. The link between mobility services and energy demand is more complex. It encompasses not only the energy efficiency of the vehicles but also the availability and efficiency of four transport modes: terrestrial public transport, air transport, private vehicles and non-motorized transport. Owing to differences in services delivered by each mode and to regional particularities, the transport modes are imperfect substitutes for one another. They are, therefore, nested in a constant elasticity of substitution function.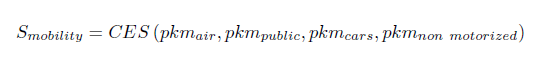
Final energy consumptions, directly borne by households, are derived from the level of housing and private vehicle services via the equation: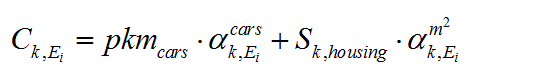
where αcars represents the mean amount of each energy needed to travel one passenger-km with the current stock of private cars, and αm2 the consumption of each energy product per square meter of housing. These parameters are maintained constant during the static equilibrium resolution; their evolution between two static equilibria is done in the dynamic modules.
Maximization Program
The representative consumer of each region maximizes its utility under two budget constraints:
- A disposable income constraint which lays down the equality between (i) the sum of purchases of non-energy goods, services and energy expenditures (induced by housing end-use equipment and private cars) and (ii) the disposable income for consuming, given a consumer price vector:
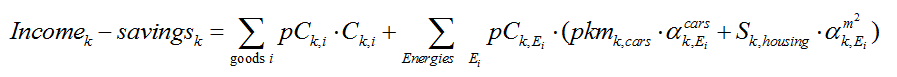
- A travel-time budget constraint imposing a ceiling to the average daily travel time of households. This constraint is justified by empirical an finding, known as the Zahavi law (Zahavi and Talvitie, 1980), which shows that the average daily travel time remains constant over decades and across a large panel of cities.
The choice between different transportation modes depends not only on their relative prices but also on the marginal efficiency of travelling-time: τk,Tj, i.e. the inverse of the marginal time used to travel one more kilometer. Each transportation mode (Tj) is thus characterized by its travel time efficiency. This parameter depends on both the average speed allowed by the available infrastructures, the speed of vehicles and the gap between modal mobility demand and the capacity of the network. When mobility demand overshoots the normal load condition of the infrastructure (CapTransportk,Tj, expressed in road-, rail- or seat-kilometers), the travel time efficiency of this transportation mode decreases. This phenomenon is due to either congestion or infrastructures' unavailability for the considered mode. Investments in transportation can thus lower the congestion of transportation networks and restore their efficiency where the amount of these investments that are allocated for each type of infrastructure is decided in the dynamic modules. In this modeling structure, mobility demand is induced by infrastructure in the long-term: the deployment of new infrastructures and the availability of more efficient vehicles push households to travel more within their income and time budget. There is thus a positive feedback loop between technical choices in the transportation sector, households' modal choices and the overall demand for mobility.
The 'travel-time budget' constraint is formalized as follows:
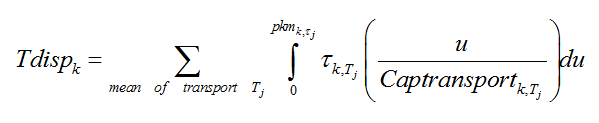
Assuming a travel time of 1.1 hours per day (in the default parameterization of the model), the total yearly time used to travel is equal to Tdispk=1.1·365·Lk, where Lk corresponds to the total population of region k.
Behavioural change
Households consumption choices are determined by current utility maximization under constraints of both revenues and time spent in transport. The utility function depends on the consumption of goods and services, from which basic needs are subtracted, and on mobility (from which basic needs are subtracted as well). See above for a detailed description. With such a representation, relative price changes induce changes in consumption choices between different types of goods.
In addition, a number of non-price mechanisms are included in the modelling framework, which can represent evolutions in lifestyles or households preferences:
- There is a saturation of the consumption volume of agricultural and industrial goods when revenues increase. A function represents the decrease of households' budget shares devoted to agricultural and industrial goods when their revenue increases. Alternative parameterizations of this function allows for the exploration of the role of different evolutions of lifestyles.
- The evolution of basic needs of mobility (exogenous trends) is used to represent the influence of urban forms and infrastructure on constrained mobility.
- A function represents the rate of private car ownership increase with increasing revenues (see Section on Transport). Alternative parameterizations of this function allows for exploration of the role of different evolutions of lifestyles and preferences concerning private mobility.
- Another function represents the rate of increase of residential floor area per capita with increasing revenues (see Section on Residential Sector). Alternative parameterizations of this function allows for the exploration of the role of different evolutions of lifestyles and preferences concerning housing.